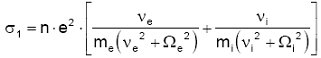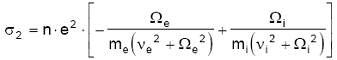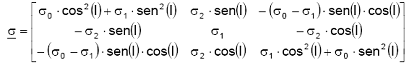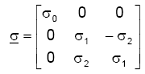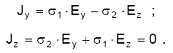CONDUTIVIDADES   IONOSFÉRICAS

A condutividade elétrica de um dado meio é determinada pela razão entre a densidade de corrente (J em A/m²) e o campo elétrico (E em V/m), definida pela forma da quação:

σ = J / E = (n e n) / E   .

(Eq. 4)

onde n é a densidade eletrônica, "e" é a carga de cada partícula sendo considerada e n é a taxa de colisão com as partículas neutras (s^-1).

Contudo, também se observa na ionosfera terrestre a presença simultânea dos campos elétricos e magnéticos. Portanto, convencionou-se apresentar a condutividade ionosférica em termos das suas três componentes da seguinte forma: ao longo do vetor campo magnético (componente longitudinal); ao longo da componente do vetor campo elétrico perpendicular ao campo magnético (componente Pedersen); e perpendicular a ambos (componente Hall).

Quando consideramos somente uma população de cargas, a componente da condutividade ao longo do campo magnético é descrita pela equação:

(Eq. 5)

No entanto, ao considerarmos diferentes populações de cargas iônicas e elétrons, podemos obter a condutividade σ₀, conhecida como condutividade direta ou longitudinal. Ela representa a condutividade paralela ao campo geomagnético, B.

(Eq. 6)

A condutividade Pedersen ou transversal (σ₁) refere-se à condutividade na direção da componente de E perpendicular a direção de B.

(Eq. 7)

A condutividade Hall (σ₂) refere-se à condutividade na direção perpendicular, simultaneamente, as direções de B e da componente de E perpendicular a direção de B.

(Eq. 8)

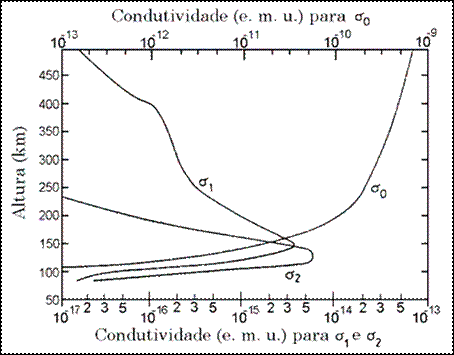
Nas equações 5, 6 e 7 acima Ω_e e Ω_i são as freqüências ciclotrônicas, n_e e n_i são as freqüências de colisão, m_e e m_i são as massas dos elétrons e íons respectivamente, "e" é a carga dos elétrons e n é a densidade de plasma.

Uma distribuição em altura calculada da condutividade na ionosfera de médias latitudes ao meio-dia é mostrada na Figura 3. Nesta figura nota-se que os picos das condutividades Pedersen e Hall ocorrem na Região E, decaindo acentuadamente acima e abaixo deste máximo. No equador magnético esse pico fica em torno de 150 km para a condutividade Pedersen e 130 km para a condutividade Hall.

Fig. 3 - Perfil de condutividade mostrando a variação das condutividades longitudinal σ₀, Pedersen σ₁ e Hall σ₂ com a altura. Para conversão 1 e.m.u. (cgs) = 10¹¹ S/m (SI).

Utilizando estas três variáveis, σ₀, σ₁ e σ₂, chegamos à equação do tensor condutividade elétrica (σ) o qual generaliza a relação de E com J, e é dado por:

(Eq. 9)

sendo "I" o ângulo da inclinação de B. Na região do equador magnético a inclinação do campo magnético é nula, logo o tensor condutividade σ nesta região resume-se a:

(Eq. 10)

Considerando somente o plano perpendicular ao campo magnético na região equatorial (eixo z está na direção vertical com sentido para cima enquanto o eixo y está na direção leste-oeste com sentido para leste), através da relação J = σ . E obtemos o seguinte conjunto de equações:

(Eq. 11)

Neste caso, devido à queda acentuada da condutividade mostrada na Figura 3, há uma inibição da corrente vertical que pode ser representada por    J_z = 0 na Eq. 11. Assim, resolvendo o sistema anterior temos:

(Eq. 12)

onde σ₃ é a condutividade Cowling, a condutividade na direção do eletrojato equatorial.